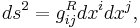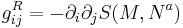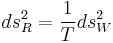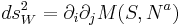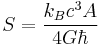Ruppeiner geometry

Ruppeiner geometry is thermodynamic geometry (a type of information geometry) using the language of Riemannian geometry to study thermodynamics. George Ruppeiner proposed it in 1979. He claimed that thermodynamic systems can be represented by Riemannian geometry, and that statistical properties can be derived from the model.

This geometrical model is based on the inclusion of the theory of fluctuations into the axioms of equilibrium thermodynamics, namely there exist equilibrium states which can be represented by points on two-dimensional surface (manifold) and the distance between these equilibrium states is related to the fluctuation between them. This concept is associated to probabilities, i.e. the less probable a fluctuation between states, the further apart they are. This can be recognized if one considers the metric tensor g_ij in the distance formula (line element) between the two equilibrium states

$ds^2 = g^R_{ij} dx^i dx^j, \,$

where the matrix of coefficients g_ij is the symmetric metric tensor which is called a Ruppeiner metric, defined as a negative Hessian of the entropy function

$g^R_{ij} = -\partial_i \partial_j S(M, N^a)$

where M is the mass (internal energy) of the system and N^a refer to extensive parameters of the system. Mathematically the Ruppeiner geometry is one particular type of information geometry and it is similar to the Fisher-Rao metric used in mathematical statistics . The Ruppeiner metric is conformally related to the Weinhold metric via

$ds^2_R = \frac{1}{T} ds^2_W \,$

where T is the temperature of the system under consideration. Proof of the conformal relation can be easily done when one writes down the first law of thermodynamics in differential forms with a few manipulations. The Weinhold geometry is also considered as a thermodynamic geometry. It is defined as a Hessian of mass (internal energy) with respect to entropy and other extensive parameters.

$ds^2_W = \partial_i \partial_j M(S, N^a)$

where N^a refer to extensive parameters of the system. It has long been observed that the Ruppeiner metric is flat for systems with noninteracting underlying statistical mechanics such as the ideal gas. Curvature singularities signal critical behaviors. In addition, it has been applied to a number of statistical systems including Van de Waals gas. Recently the anyon gas has been studied using this approach.

Application to black hole systems

In the last five years or so this geometry has been applied to black hole thermodynamics with some results physically relevant. The most physically significant case is in the Kerr black holes in higher dimensions where the curvature singularity signals thermodynamic instability as found earlier by conventional method.

Black hole's entropy is given by the well-known Bekenstein-Hawking formula

$S =\frac{k_B c^3 A}{4G \hbar}$

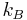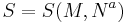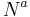where $k_B$ is Boltzmann's constant, $c$ the speed of light, $G$ the Newton's constant and $A$ is the area of the event horizon of the black hole. Calculating the Ruppeiner geometry of the black hole's entropy is, in principle, straightforward but important the entropy should be written in terms of extensive parameters, $S= S(M, N^a)$ where $M$ is ADM mass of the black hole and $N^a$ conserved charges and $a$ runs from 1 to n. The signature of the metric reflects the sign of the hole's specific heat. For Reissner-Nordström black hole, the Ruppeiner metric has a Lorentzian signature which corresponds to the negative heat capacity it possess, while for the BTZ black hole we have a Euclidean signature. This cannot be done for the Schwarzschild black hole because its entropy is

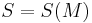$S = S(M)$ which renders the metric degenerate.

References

Ruppeiner, George (1995), "Riemannian geometry in thermodynamic fluctuation theory", Reviews of Modern Physics 67 (3): 605–659, Bibcode 1995RvMP...67..605R, doi:10.1103/RevModPhys.67.605 .

Ruppeiner geometry

Application to black hole systems

References

External links